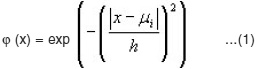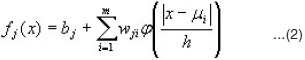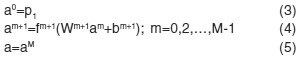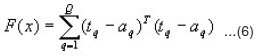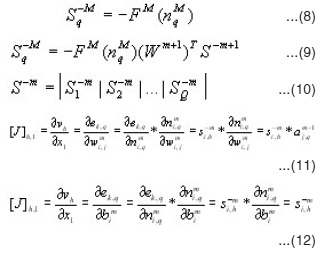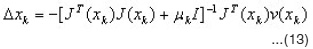Approaches in RSA Cryptosystem Using Artificial Neural Network

Siamak Haghipour and Babak Sokouti*

Faculty of Engineering, Islamic Azad University - Tabriz Branch, Tabriz, (Iran).

ABSTRACT:

RSA cryptosystem, the first public key cryptography presented in 1977. Neural networks are often used as a powerful discriminating estimator for tasks in function approximation. This paper describes a neural-network-based method relies on Radial Basis Function and Levenberg-Marquardt Backpropagation for estimating the behavior of the function used in RSA cryptosystem to calculate the function. The difficulty of the RSA cryptosystem relies on the difficulty of the factorization, to have the RSA cryptosystem broken, it suffices to factorize N which is the product of two prime numbers p, q (N=p.q). This will be equivalent to calculate the Euler function φ(N)=(p-1)(q-1) .

KEYWORDS: Artificial Neural Network; Factorization; Radial Basis Function; Back Propagation; RSA Cryptosystem

Copy the following to cite this article: Haghipour S, Sokouti B. Approaches in RSA Cryptosystem Using Artificial Neural Network. Orient. J. Comp. Sci. and Technol;1(1)

Copy the following to cite this URL: Haghipour S, Sokouti B. Approaches in RSA Cryptosystem Using Artificial Neural Network. Orient. J. Comp. Sci. and Technol;1(1). Available from: http://www.computerscijournal.org/?p=2079

Introduction

The science of encrypting and decrypting messages by using mathematic to achieve information secrecy is Cryptography which enables us to store or transmit the sensitive information via an insecure channel (i.e. internet) that cannot be read and understood by anyone except the intended recipient. A simple cryptosystem consists of a plain text, cipher text, an encryption key, encryption algorithm, a decryption key and decryption algorithm as shown in Fig. 1.

There are two general forms of cryptosystems: symmetric (secret-key) and asymmetric (public-key) cryptosystems.

In the symmetric cryptosystem, the encryption and decryption keys are the same and the entity who generates the key must share the encryption key with the entity that will be able to decrypt the encrypted message; the security of the cryptosystem relies on keeping the encryption key secret. Suppose x as plain text, y as cipher text and k as the encrypting and decrypting key (a symmetric key), the sender will produce the cryptogram y = E_k(x) that is transmitted through the insecure channel to the receiver that decrypts the message and deduce the original plaintext x = D_k(y) = D_k ( E_k(x) ). The disadvantage of this cryptosystem is the requirement for providing a secure channel for transmitting the shared key. In public-key cryptosystem, the encryption and decryption use different keys and there is no need for encryption key to be kept secret and the entity who will receive the cipher text is able to deduce the message by corresponding decryption key; there is no computational way of obtaining decryption key from the encryption key.

The RSA

The most popular public-key cryptosystem is the RSA, named for its creators: Rivest, Shamir and Adleman¹ proposed in 1977 that can be used for both encryption and digital signatures in the literature. Since then several public-key systems have been proposed^2,6 that their security relies on the hard computational problems.^3,6 The RSA cryptography is based on the notion of one-way trapdoor function,^2,7 gets its security from the difficulty of factoring integer numbers. For implementing an RSA cryptosystem, the generation of two keys are needed; first of all two large prime numbers p, q are chosen.^{8, 9} (This can be done by Monte-Carlo prime number finding algorithm), then their product N = p.q and the Euler function will be computed. The next step is to find e and d. A random integer number e<Ҩ(N) is chosen such that gcd (Ҩ(eN)=1, then the Extended Euclid Algorithm is used to find the integer decryption key from e.d = 1mod (Ҩ (N)). For the encryption process the sender will encrypt the confidential message with the public key e in the following form of a modular exponentiation:

C ← M^e mod (N)

And for the decryption process the receiver will decrypt the encrypted message by the decryption key d again in the form of a modular exponentiation:

M ← C^d mod (N) = (M^e)^d mod(N) = M mod (N)

Any adversary knows the public keys pairs (N, e) and the structure of the system and is familiar with a modular exponentiation equation. The most well known attacks against the RSA cryptosystem is to factor N to its prime integer numbers that computationally is impossible; it is also possible to attack the RSA by guessing the value of Euler function Ҩ(N) = (p – 1)(q – 1) that is not easier than factoring N^10,11 Though it is also possible for the adversary to use the Brute Force attack, means to try all the decryption keys which are less than Ҩ(N) to obtain the intended message, it is less efficient than factoring modulus N. Neural networks are used to determine the Euler function Ҩ(N) = (p – 1)(q – 1) from inputting N = p.q where p and q are prime numbers and the neural networks output will be Ҩ(N) = (p – 1)(q – 1).

Figure 1: A simple cryptosystem diagram Click here to View figure

 

Figure 2: Feed forward Neural Network Scheme Click here to View figure

 

Neural Network Techniques The RBF Algorithm

The Radial Basis Function Networks are similar to the biological networks behavior; primarily the hidden layers contain almost sensing units and the output layer contains linear units. Usually for a common RBF network the transfer function in the hidden layer is a Gaussian function that is introduced in equation (1) as below:

where as, µ_i ∈ R^d is called the center vector, and h ∈R is called the kernel width (or smoothing parameter). The basic RBF network provides a nonlinear transformation of a pattern x º R^d ® R^e according to equation (2):

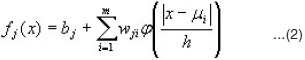
where m is the number of basis functions, wji is a weight, bj is a bias.^12,15

The Levenberg-Marquardt (LM)

Back Propagation Algorithm

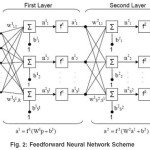
A variation of the standard back propagation algorithm is Levenberg-Marquardt that is used for training the multilayer networks and is preferably used over the standard back propagation; this algorithm is the fastest for multilayer neural networks.^16,17 When the network is a single layer one it is easy to find the optimum solution in selecting the learning rate but it has more than one hidden layer, it gets complex. This needs for the learning rate being able of changed between the steepest descent and the Newton algorithm depending on weather the value of the function is near the optimum solution or not; The Levenberg-Marquardt algorithm has this property. The disadvantage of the Levenberg-Marquardt over the standard back propagation is the storage requirement for approximate Hessian matrix (r_xr matrix) where r is the number of parameters (weights and biases) in the network. A Feed forward Multilayer Neural Network Scheme is presented in Fig. 2. Suppose that pattern inputs (p_q) and corresponding target outputs (t_q) are given as {p₁,t₁},{p₂,t₂},…,{p_Q,t_Q} the iteration of the Levenberg-Marquardt algorithm will be as follows:

All inputs are given to the network and the corresponding network outputs and error will be computed:

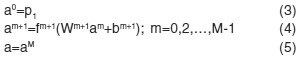
Where a⁰ is the output for input layer p₁ , a^m+1 is the output for layer m+_1, f^m+1 the transfer function for layer m+1, W^m+1 is the weights matrix and b^m+1 is the bias vector, a^M is the last layer’s output.

Table 1: Results for networks trained with RBF algorithm and data set N = p.q ≤ 1000 Click here to View Table

 

Table 2: Results for networks trained with RBF algorithm and data set N = p.q ≤ 1000 Click here to View Table

 

The squared errors over all inputs will be computed from the following equation:

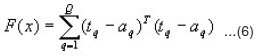
Jacobean matrix (J(x)) and sensitivities (S^-M) with the recurrence relations will be computed as follows

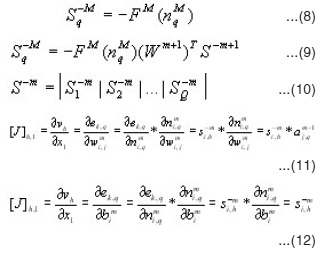
where S^-m is the Marquardt sensitivities matrix and [J]_h,l is the element of the Jacobean matrix that corresponds to the h^th row and l^th column.

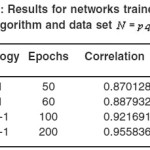
∆X_k will be obtained from the below equation

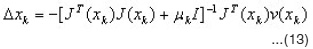
X_k + ∆X_k will be recalculated to obtain the sum of squared errors, if it is smaller than the on in step 2 then divide µ(i.e. 0.01) by ϑ (larger than

1, i.e. 10) then let X_k+1 = X_k + ∆X_k and start from step 1; otherwise if the sum is not reduced then multiply µ(i.e. 0.01) by ϑ (larger than 1, i.e. 10) and start from step 4.

This process will be continued until the difference between the network response and the target reduced to the error goal that means the algorithm has been converged.

Experimental Results

The experimental results are made by using Neural Networks in MATLAB interface in Windows XP operating system SP2. The Neural Networks used are:

Radial Basis Function Neural Network (RBF).¹⁸

Levenberg- Marquardt Back propagation Neural Network.¹⁶

Standard Back propagation Neural Network. ¹⁹

All the above methods were tested and their correlation rates for their performance were calculated with a large range of parameter. However the results showed some significant differences between the Neural Network models. The standard Back propagation has big difficulties in the training stage most of the times; Levenberg-Marquardt Back propagation managed to be the fastest RBF Neural Network is good in function approximation but it has the limitations of a one-hidden layer Neural Networks.

According to the network structure, choosing optimal network architecture for the related problem is very difficult and is a problem in recent years.

Table 3: Results for networks trained with RBF algorithm and data set N = p.q ≤ 2000 Click here to View Table

 

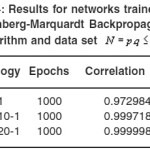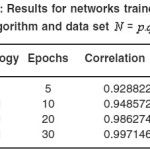
Table 4: Results for networks trained with Levenberg-Marquardt Back propagation algorithm and data set N = p.q ≤ 2000 Click here to View Table

 

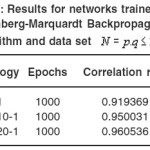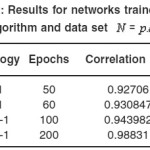
Table 5: Results for networks trained with Levenberg-Marquardt Back propagation algorithm and data set N = p.q ≤ 1000 Click here to View Table

 

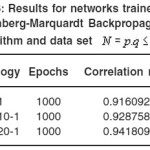Table 6: Results for networks trained with Levenberg-Marquardt Back propagation algorithm and data set N = p.q ≤ 1000 Click here to View Table

 

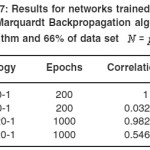Table 7: Results for networks trained with Levenberg-Marquardt Back propagation algorithm and RBF algorithm and 66% of data set N = p.q ≤ 1000 Click here to View Table

 

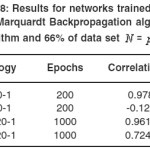Table 8: Results for networks trained with Levenberg-Marquardt Back propagation algorithm and RBF algorithm and 66% of data set N = p.q ≤ 2000 Click here to View Table

 

A large variety of network topologies were used in t his approach. By using different network topologies, the obtained results were considerable; and after extensive testing, a conclusion can be made that 2 hidden layers networks were much easier in train and much accurate in performance. Here the input patterns were and the target outputs were Ҩ(N) = (p – 1)(q – 1) in which the network tries to learn the function that transfers N to Ҩ(N)

(i.e. N = pq → Ҩ(N) = (p – 1)(q – 1) and predicts the output Ҩ(N) by taking the input N to overcome the RSA problem.

To test the network performance here, the correlation rate value is considered as where the value is near the integer number 1 or -1 the there is a good prediction of the output and where the value is near zero there is not a good prediction in that network. It is important that the good correlation rate value plays an outstanding role as the computation of the function can be solved by a second degree polynomial equation since Ҩ(N) =N-p-q+1. In this test the limited number of data set N = pq ≤ 100, N – pq ≤ 1000, N = pq ≤ 2000) is considered to find out the related neural networks’ performance.

In table 1 we can see the results of the network trained by RBF algorithm with a data set N = pq ≤ 100. In Table 2, 3 the larger prime numbers are tried with a significant change in the network topology. These test are also performed for the Levenberg-Marquardt Back propagation that can be seen in Table 4,5,6 that can be seen that a 2 hidden layer performance in prediction is better that the one hidden layer network. Finally, network performance is done by the data set 33% for Test set and 66% of the data set as Train set, gives us the results exhibited in Table 7, 8. As it is clear the Levenberg-Marquardt Back propagation Network is able not only to adapt to train data but to reach good results to test sets in comparison with the RBF Neural Network.

Conclusion

In this paper, the approaches of one-hidden layer (RBF) and 2-hidden layer (Levenberg-Marquardt Back propagation) Neural network against the RSA cryptosystem were employed and from the illustrated results it is clear that though the RB neural network is very good at function estimation, in the RSA problem its usage is not reached in good results. Additionally the 2-hidden layer neural network can be employed for this purpose to reach better results according to the network topology and the training of Levenberg-Marquardt algorithm parameters. In general, the RSA problem could be solved if the correlation rate value reaches the number 1. There is still a long way to employ the real power of the neural networks.

In conclusion, the approaches of neural networks in the RSA problem are promising though many works is needed to be done.

References

1. R.L. Rivest, A. Shamir, and L. Adleman. A method for obtaining digital signatures and public-key cryptosystems. Communications of the ACM, 21(2):120–126, (1978).
2. W. Diffie and M. Hellman, New Directions in Cryptography, IEEE Trans. I.T., 22, 644-654 (1976).
3. T. El Gamal, A Public Key Cryptosystem and a Signature Scheme Based on Discrete Logarithms, IEEE Trans. I.T., 31, 469–472 (1985).
4. N. Koblitz, Elliptic Curve Cryptosystems, Math. Comp.,48,203–209 (1997).
5. R.C. Merkle and M.E. Hellman, Hiding Information and Signatures in Trapdoor Knapsacks, IEEE Trans. I.T., 24, 525–530 (1978).
6. S.C. Pohlig and M. Hellman, An Improved Algorithm for Computing Logarithms over GF(p) and its Cryptographic Significance, IEEE Trans. I.T.,24,106–110 (1978).
7. W. Diffie and M. Hellman. Multiuser cryptographic techniques. In Proceedings of AFIPS 1976 NCC, pages 109–112. AFIPS Press, Montvale, N.J., (1976).
8. R. Solovay and V. Strassen, A Fast Monte Carlo Test for Primality, SIAM J. Comput., 6(1), 84–85 (1977).
9. Menezes, P. van Oorschot, and S. Vanstone. Handbook of Applied Cryptography. CRC, (1996).
10. C.K. Wu and X.M. Wang, “Determination of the True Value of the Euler Totient Function in the RSA Cryptosystem from a Set of Possibilities,” Electronics Letters, 29(1), 84–85 (1993).
11. G.L Miller, Rieman’s Hypothesis and Tests for Primality, Journal of Computer and System Sciences,13,300–317 (1976).
12. Cybenko, G., Approximation by super-positions of a sigmoidal function. Math. Controls, Signals, Syst.,2,303-314 (1992).
13. Hartman, K., Keeler, J. D. and Kowalski, J. M., Layered Neural Networks with Gaussian hidden units as universal approximation. Neural Computation,2,210-215 (1990).
14. Hornik, K., Sitnchcombe, M. and White, H., Multilayer feedforward networks are universal approximators. Neural Networks, 2, 359-366 (1989).
15. Schalkoff Robertj, Artificial Neural Networks, Mcgraw Hall, (1997).
16. Hagan, M., and M. Menhaj,: Training feedforward networks with the Marquardt algorithm. IEEE Transactions on Neural Networks, 5(6):989-993, (1994).
17. Hagan, M., H. Demuth and M. Beale,: Neural network design. PWS Publishing Co., Boston, (1996).
18. S. Haykin, Neural Networks, (New York: Macmillan College Publishing Company, (1999).
19. D.E. Rumelhart, G.E. Hinton and R.J. Williams, Learning Internal Representations by Error Propagation, In D.E. Rumelhart and J.L. McClelland (Eds.) Parallel distributed processing: Explorations in the microstructure of cognition, Cambridge, MA,MIT Press, 1, 318–362 (1986).

---

This work is licensed under a Creative Commons Attribution 4.0 International License.