Prime Cordial Labeling in Context of Ringsum of Graphs

A. B. Patel¹ and V. B. Patel²

¹Mathematics, L. D. College of Engineering, Ahmedabad, Gujarat, India.

²Department of Mathematics, Dharmsinh Desai University, Nadiad, Gujarat, India.

Corresponding Author E-mail: drabpatel@ldce.ac.in

ABSTRACT:

A bijection f from the vertex set V of a graph G to {1,2, …, |V|} is called a prime cordial labeling of G if each edge uv is assigned the label 1 if gcd (f(u), f(v)) = 1 and 0 if gcd (f(u), f(v)) > 1, where the number of edges labeled with 0 and the number of edges labeled with 1 differ at most by one. In this paper I have proved four new results admitting Prime cordial labeling.

KEYWORDS: Prime Cordial Labeling; Ringsum of a Graph

Copy the following to cite this article: Patel A. B, Patel V. B. Prime Cordial Labeling in Context of Ringsum of Graphs. Orient.J. Comp. Sci. and Technol; 10(1).

Copy the following to cite this URL: Patel A. B, Patel V. B. Prime Cordial Labeling in Context of Ringsum of Graphs. Orient.J. Comp. Sci. and Technol; 10(1). Available from: https://bit.ly/49vCIZs

Introduction

The graphs considered here are finite, connected, undirected and simple. The vertex set and edge set of a graph G are denoted by V (G) and E(G) respectively. For various graph theoretic notations and terminology we follow Gross and Yellen³. A dynamic survey of graph labeling is published and updated every year by Gallian². The concept of Sundaram et al ⁴ introduced the concept of prime cordial labeling.

Definition 1

Ring sum G₁ ⊕ G₂ of two graphs G₁ = (V₁, E₁) and G₂ = (V₂, E₂) is the graph G₁⊕ G₂ = (V₁ ∪  V₂, (E₁  E₂) − (E₁ ∩ E₂)).

Main Results

Theorem 1

The graph C_n ⊕ K_1,n is Prime cordial graph.

Proof. Let V (G) = V₁∪V₂, where V₁ = {u₁, u₂, . . . , u_n} be the vertex set of C_n and V₂ = {v = u₁, v₁, v₂, . . . , v_n}be the vertex set of K_1,n, where v₁, v₂, . . . , v_n are pendant vertices. Note that |V (G)| = |E(G)| = 2n.

Define labeling function f : V→ {1,2,….,2n}  as follows.

For all 1 ≤ i ≤ n.

f (u_i) = 2i,

f (v_i) = 2i – 1.

Then in we have e_f (0) = e_f (1) = n.

Therefore |e_f (0)-e_f (1)| ≤1

Hence C_n ⊕ K_1,n is a Prime cordial graph.

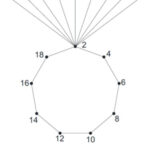
Example 1. Prime cordial labeling of the graph C₉ ⊕ K_1,9 is shown in Figure 1.

Figure 1 Click here to view Figure

Theorem 2

The graph G ⊕K_1,n is Prime cordial, where G is cycle C_n having one chord, where chord forms a triangle with two edges of the cycle.

Proof. Let G be the cycle C_n with one chord and Let e = u₂u_n be the chord in G.

Let V = V₁ ∪ V₂, where V₁ = {u₁, u₂, . . . , u_n} be the vertex set of C_n and V₂ = {v, v₁, v₂, . . . , v_n} be the vertex set of K_1,n. Here v is the apex vertex and v₁, v₂, . . . , v_n are pendant vertices. Note that v = u₁. |V (G)| = 2n, |E(G)| = 2n + 1.

Define labeling function f : V → {1,2,…, 2n} as follows.

For all 1 ≤ i ≤ n.

f (u_i) = 2i,

f (v_i) = 2i – 1.

Therefore |e_f (0)-e_f (1)| ≤1

Hence G ⊕ K_1,n is Prime cordial, where G is cycle C_n having one chord.

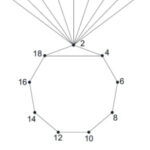
Example 2. Prime cordial labeling of ring sum of the graph cycle C₉ with one chord and K_1,9 is shown in Figure 2.

Figure 2 Click here to View Figure

Theorem 3

The graph G ⊕ K_1,n is Prime cordial for all n, where G is cycle having twin chords C_n,3.

Proof. Let G be the cycle having twin chords C_n,3, e = u₂ u_n and e’ = u₃ u_n be the chords in G. Let V = V₁ ∪ V₂, where V₁ = {u₁, u₂, . . . , u_n} be the vertex set of G and V₂ = {v, v₁, v₂, . . . , v_n} be the vertex set of K_1,n. Here v is the apex vertex and v₁, v₂, . . . , v_n are pendant vertices. Note that v = u₁. Also, |V(G ⊕ K_1,n)| = 2n, |E(G ⊕ K_1,n)| = 2n + 2.

Define f : V → {1,2,…, 2n} we conceive the below cases.

Case 1: n = 5

For all 1 ≤ i ≤ n,  

f(u₄) = 5,

f(u₅) = 8,

f (u_i) = 2i, 1 ≤ i ≤ 3,

f(v₅) = 10,

f (v_i) = 2i – 1, 1 ≤ i ≤ 4.

Therefore e_f (0) = e_f (1) = n + 1.

Case 2: for all n except n = 5

f (u_n) = 8,

f (u_i) = 2i, 1 ≤ i ≤ 3,

f (u_i) = 2i – 7, 4 ≤ i ≤ n – 1,

Assign the remaining vertices of star graph in any order.

Therefore e_f (0) = e_f (1) = n + 1.

Hence, G ⊕ K_1,n is Prime cordial for all n, where G is cycle having twin chords C_n,3.

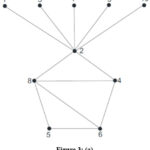
Example 3(a). Prime cordial labeling of ring sum of the graph cycle C₅ with one chord and K_1,5 is shown in Figure 3(a).

Figure 3:A Click here to View Figure

Example 3(b). Prime cordial labeling of ring sum of the graph cycle C₇ with one chord and K_1,7 is shown in Figure 3(b).

Figure 3: B Click here to View Figure

Theorem 4

P_n⊕ K__1,n is Prime cordial.

Proof. Let V (G) = V₁∪V₂, where V₁ = {u₁, u₂, . . . , u_n} be the vertex set of P_n, V₂ = {v, v₁, v₂, . . . , v_n} be the vertex set of K_1,n, where v₁, v₂, . . . , v_n are pendant vertices and v = u₁. Note that |V (G)| = 2n, |E(G)| = 2n-1.

We define labeling function f : V (G) → {F₀, F₁, F₂, . . . , F_2n}, as follows.

f (u_i) = 2i – 1, 1 ≤ i ≤ n.

f (v_i) = 2i, 1 ≤ i ≤ n.

Therefore |e_f (0) – e_f (1)| ≤ 1 .

Hence, P_n ⊕ K₁,n is Prime cordial.

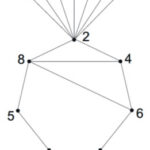
Example 4: Prime cordial labeling of P₅ ⊕ K₁,₅ is shown in figure 4.

Figure 4 Click here to View Figure

References 

1. L. Cahit , Cordial Graphs: A weaker version of graceful and Harmonic Graphs, Ars Combinatoria, 23, (1987), 201 − 207.
2. J. A. Gallian, ”A dynamic survey of graph labeling”, The Electronics Journal of Combinatorics, 16(2013), #DS6 1 − 308.
3. J. Gross and J. Yellen, Graph Theory and its Applications, CRC Press, 1999.
4. M. Sundaram, R. Ponraj and S. Somasundaram, Prime cordial labeling of graphs, Journal of Indian Academy of Mathematics, 27(2005) 373-390.
5. A. H. Rokad and G. V. Ghodasara, Fibonacci Cordial Labeling of Some Special Graphs, Annals of Pure and Applied Mathematics, Vol. 11, No. 1, 2016, 133 − 144.
6. R. Sridevi, S. Navanaeethakrishnan and K. Nagarajun, Super Fibonacci Graceful Label- ing, International Journal Mathematical Combinatorics, Vol.3(2010), 22 − 40.
7. R. Sridevi, K. Nagarajun, A. Nellaimurugan, S. Navanaeethakrishnan, Fibonacci divisor cordial graphs, International Journal of Mathematics and Soft Computing,Vol.3,No.3(2013), 33 − 39.
8. S. K. Vaidya and P. L. Vihol, Fibonacci and Super Fibonacci Graceful Labeling of Some Graphs studeies in mathematical sciences, Vol.2, No. 2,2011, pp. 24-35.
9. S. K. Vaidya and P.L. Vihol Prime cordial labeling for some Cycle Related Graphs, Int. J. Open Problems Compt., Maths, Vol-3, No-5, December 2010, ISSN  1998- 6262.
10. A. H. Rokad and G. V. Ghodasara, Prime Labeling in Context of Ring Sum of Graphs, International Journal of Science and Research, Vol. 4 Issue 12, Dec. 2015, Page 390-392.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.