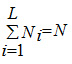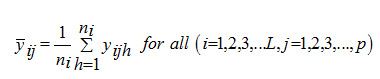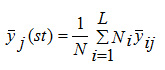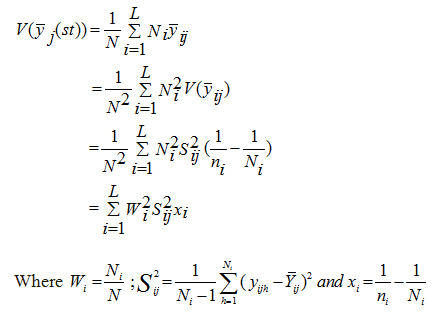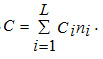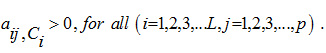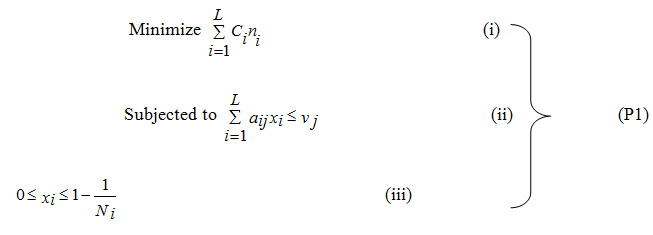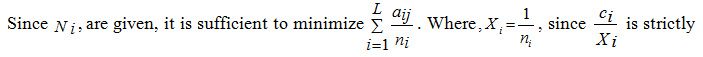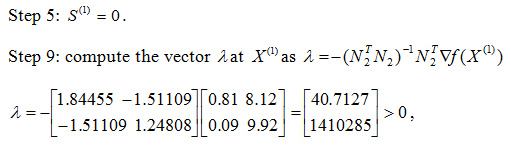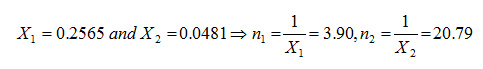Optimal Allocation of Stratified Sampling Design Using Gradient Projection Method
M. A. Lone, S. A. Mir , Imran Khan and M. S. Wani
Division of Agri.stat, SKUAST-K
DOI : http://dx.doi.org/10.13005/ojcst/10.01.02
Article Publishing History
Article Received on : January 26, 2017
Article Accepted on : February 08, 2017
Article Published : 10 Feb 2017
Article Metrics
ABSTRACT:
This article deals with the problem of finding an optimal allocation of sample sizes in stratified sampling design to minimize the cost function. In this paper the iterative procedure of Rosen’s Gradient projection method is used to solve the Non linear programming problem (NLPP), when a non integer solution is obtained after solving the NLPP then Branch and Bound method provides an integer solution.
KEYWORDS:
Stratification; Optimal allocation; nonlinear programming; Gradient projection method; Branch and Bound method and integer allocation
Copy the following to cite this article:
Lone M. A, Mir S. A, Khan I, Wani M. S. An insight into IP Addressing. Orient.J. Comp. Sci. and Technol;10(1)
|
Copy the following to cite this URL:
Lone M. A, Mir S. A, Khan I, Wani M. S. An insight into IP Addressing. Orient.J. Comp. Sci. and Technol;10(1). Available from: http://www.computerscijournal.org/?p=4680
|
Introduction
One of the areas of statistics that is most commonly used in all fields of scientific investigation is that of stratified sampling. In order to achieve greater precision of the estimate it is desirable to decrease the heterogeneity of the population units. This is achieved by a technique known as stratification, in which the entire population is divided into a number of sub population called strata. Generally, the stratification is done according to administrative grouping, geographic regions and on the basis of auxiliary characters. These sub-population are non-overlapping and together they comprise the whole of the population. These strata are so formed that they are homogeneous within and heterogeneous between. When the strata have been determined, a sample is drawn from each stratum, the drawing being made independently in different strata. In stratified sampling the most important consideration is the allocation of sample sizes in each stratum either to minimize the variance subject to cost or minimize cost subject to variance The problem of optimally choosing the sample sizes is known as the optimal allocation problem. The problem of optimal allocation for univariate stratified population was first considered by Neyman (1934) .In univariate stratified random sampling for one characteristics, the sample size and its allocation is cited in Cochran (1977), Sukhatme et al. (1984) and Thompson (1997). The allocation problem becomes more complicated in multivariate surveys because in univariate an allocation that is optimal for one characteristic may be far from optimal for other characteristics. Some of the author who addressed the problem of obtaining a compromise allocation that suits well to all the characteristics are Ghosh (1958), Yates (1960), Aoyama (1963), Hartley (1965), Folks and Antle (1965), Gren (1966), Chatterjee (1972), Chromy (1987), Wywial (1988), Bethel (1989), kreienbrock (1993), Khan et al. (1997,2003). Ahsan et al. (2005), Kozak (2006), Ansari et al. (2009), Optimum allocation has been stated as a non-linear mathematical programming problem in which the objective function is the variance subject to a cost restriction or vice versa. This problem has been solved by using Lagrange’s multiplier method, see Sukhatme et al.(1984) or the Cauchy-Schwarz inequality, see Cochran(1977) for univariate case and Arthanari and Dodge (1981) for multivariate one, both from deterministic point of view. In this paper objective is to use Rosen’s Gradient projection method to determine the optimal allocation of sample sizes in stratified sampling design.
Formulation of the problem
Let us assume that there are p characteristics under study and be the jth characteristics to be considered. Suppose we have L strata, and N be the total population,units in the ith stratum such that Also, we assume that ηi samples are drawn independently from each stratum and y–ij is an unbiased estimate of y–ij such that
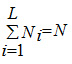
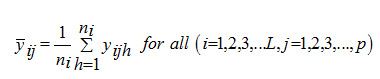
Where yijh is the observed value for Yj in the ith stratum for the hth sample unit.
Then y–j(st) given by
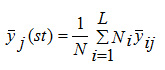
is an unbiased estimate of population mean Y– . The precision of this estimate is measured by the variance of the sample estimate of the population characteristics.
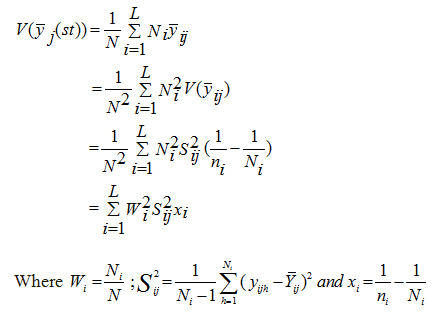
Let aij = W2jS2ij. Also, let Cj be the cost of sampling all the p characteristics on a single unit in the ith stratum. The total variable cost of the survey assuming linearity is Assume that
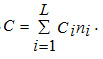
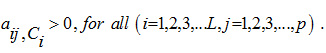
Here we consider the problem of deriving statistical information on population characteristics, based on sample data, and can be formulated as an optimization problem, in which we determine optimum allocation of sample size , ,such that cost of the survey is minimized. The multivariate sample design and optimization has been treated as a mathematical programming problem (Arthanari and Dodge (1981) .Thus the problem of allocation can be stated as (see Sukhatme et al. (1984) and Arthanari and Dodge (1981).
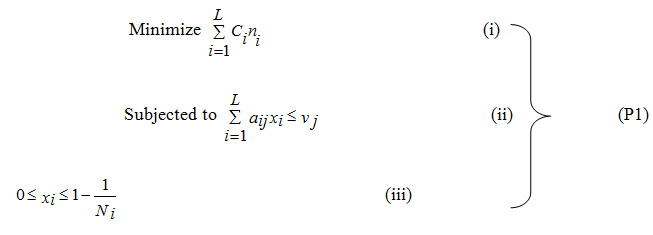
Where vj is the allowable error in the estimate of the jth characteristic. Here objective function as well as set of constraints is linear but the restriction (3) is non linear. The problem (P1) can also be written as

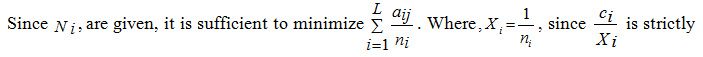
convex for cj >0 because of this objective function is strictly convex and the set of constraints provides a bounded convex feasible region and an optimal solution will also exit. Dalenius (1957) proposed a graphical solution to the problem for two characteristics. Kokan and khan (1967) have proved the existence and uniqueness of the solution and have given the optimal solution through iterative procedure. Chatterjee (1968) gives an algorithm to solve the problem. In 1960, Rosen developed the Gradient Projection method for linear constraints and later in 1961, generalized it for nonlinear constraints. It uses the projection of the negative gradient in such away that improves the objection function and maintains feasibility. Although the method has been described by Rosen for a general non linear programming problem, its effectiveness is confined primarily to problems in which the constraints are all linear. The procedure involved in the application of the gradient projection method can be described in the following Algorithm.
Algorithm of Gradient Projection method

Numerical illustration
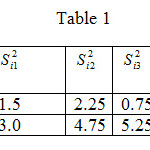
The given data has been taken from Mohd.Vaseem Ismail et al (2010). The population contains 450 units, the stratum weights and stratum variance of a population which has been divided into two strata with three characteristics under study is given below in the table 1


Solution procedure



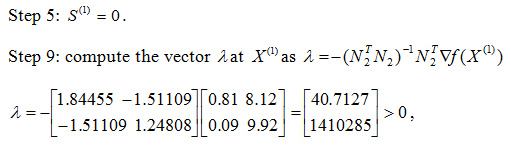
The non-negative value of λ indicates that we have reached the optimum point and the optimum value is Min Z= 94.85.
Step 11: The optimum allocation is
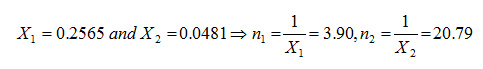
Since η1 and η2 are required to be the integers. For practical purpose if the solution is non integer then the NLPP is solved using Branch and Bound method instead of rounding the non integer sample sizes to the nearest integral values. However in some situation for small samples the rounded off allocation may become infeasible and non optimal In order to get the integer value we use Branch and bound method as given below for problem (p1). Using LINGO-13.0, we obtain the integer optimum allocation as η1=4 and η2= 21 and the optimal value is 96.
Conclusion
This paper concludes that when a non integer solution exists after solving the NLPP then Branch and Bound method is used to obtain the integer solution of the NLPP
References
- Ahsan, M. J., Najmussehar and Khan ,M. G.M. Mixed allocation in stratified sampling .Aligrah Journal of Statistics sciences 25(2005)87-97.
- Ansari A.H., Najmussehar and Ahsan M.J. On Multiple Response Stratified Random Sampling Design, International Journal of Statistical Sciences, 1(2009) 45-54.
- Aoyama H. Stratified Random Sampling with Optimum Allocation for Multivariate Populations, Annals of the institute of statistical Mathematics. 14(1963)251–258.
CrossRef
- Arthanari ,T.S., and Dodge, Y.Mathematical programming in statistics. New York: John Willy(1981).
- Bethel J. Sample Allocation in Multivariate Surveys. Survey Methodology, 15(1989) 40-57 .
- Chatterjee, S. A study of optimum allocation in multivariate stratified surveys. Skandinavisk Actuarietidskrift55(1972)73-80.
- Chatterjee, S.Multivariate stratified surveys.Journal of American statistics Association. 63(1968)530-535.
- Chromy, J. R. Design Optimization with Multiple Objectives. In: Proceedings of the Survey Research Methods section. Alexandria, VA: American Statistical Association,(1987)194–199 .
- Cochran W.G. Sampling Techniques, 3rd edition. John Wileyand Sons, New York(1977).
- Dalenius. Sampling in Sweden. Contributions to the Methods and Theories of Sample Survey Practice. Stockholm: Almqvist and Wicksell(1957).
- Folks, J.K., Antle, C.E. Optimum allocation of samplingunits to the strata when there are R responses of interest. Journal of American Statistical Association 60 (1965) 225-233.
- Ghosh,S.P. A note on stratified random sampling with multiple characters. Calcutta Statistical Bulletin 8 (1958) 81-89.
CrossRef
- Gren , J. Some Application of Non-linear Programming in Sampling Methods, Przeglad Statystyczny, 13(1966)203–217 (in Polish).
- Hartley H.O. Multiple purpose optimum allocation in stratified sampling, in : Proceedings of the American Statistical Association, Social Statistics Section. Alexandria, VA: American Statistical Association, (1965)258-261.
- Khan. M.G.M., and Ahsan, M. J., and Jahan, N. An optimal multivariate stratified sampling using dynamic programming .Australian & New Zealand of statistics 45(2003) 107-113.
- Khan. M.G.M., and Ahsan, M. J., and Jahan, N. Compromise allocation in multivariate stratified sampling : An integer solution .Naval Research Logistics 44(1997)69-79.
CrossRef
- Kokan, A. R. and Khan, S. U. Optimum allocation in multivariate surveys: An analytical solution.Journal of Royal Statistical Society, Ser. B, 29(1967) 115-125.
- Kozok M. On sample allocation in multivariate surveys, Communication in Statistics-Simulation and Computation, 35(2006) 901-910.
CrossRef
- Kreienbrock, L . Generalized measures of dispersion to solve the allocation problem in multivariate stratified random sampling . Cmmunication in Statistics : theory and methods 22(1993) 219-239.
CrossRef
- Lingo 13.0, LINDO inc.ltd.
- Mohd.Vaseem Ismail et al.Multi-objective convex programming problem arising in multivariate sampling. International Journal of Engineering Scienceand Technology2(2010)291-296.
- Neyman, J. On the two Different aspects of the representative method: The method of stratified sampling and the method of purposive selection. Journal of Royal Statistical Society 97(1934)558-625.
CrossRef
- P. V. Sukhatme, B. V. Sukhatme, Sukhatme, C. Asok. Sampling theory of Surveys with Applications. Iowa State University Press, Iowa, U. S. A. and Indian Society of Agricultural Statistics, New Delhi, India (1984).
- Rosen, J.B. The gradient projection method For Nonlinear Programming, Part i, linear constraints. SIAM journal of Applied Mathematics8 (1960)181-219.
CrossRef
- Rosen, J.B. The gradient projection method For Nonlinear Programming, Part ii, Nonlinear constraints. SIAM journal of Applied Mathematics9 (1961)514-553.
CrossRef
- Thompson, M.E. Theory of Sample Surveys. Chapman & Hall (1997).
CrossRef
- Wywial J. Minimizing the Spectral Radius of Means Vector from Sample Variance–covariance Matrix Sample Allocation between Strata, Prace Naukowe AkademiiEkonomicznej we Wroclawiu. Wroclaw, Poland, 404 (1988) 223–235 (in Polish).
- Yates, F. Sampling Methods for Censuses and Surveys. 3rd ed. London: Charles Griffin (1960).

This work is licensed under a Creative Commons Attribution 4.0 International License.