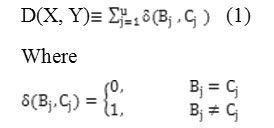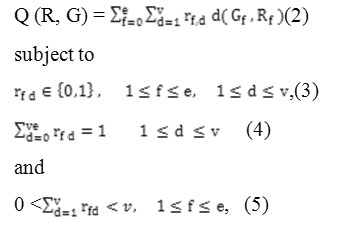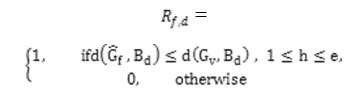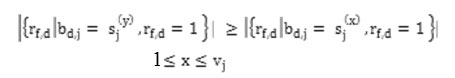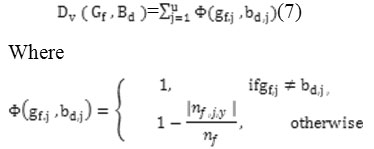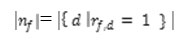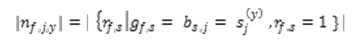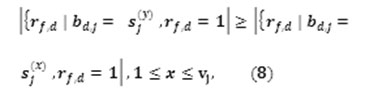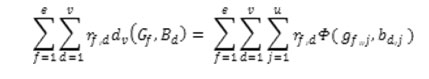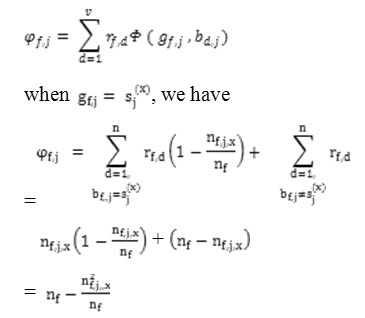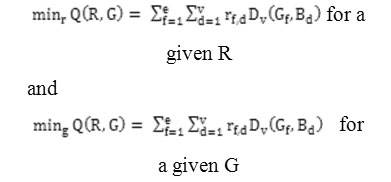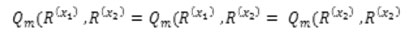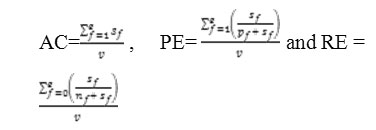On the Consequence of Variation Measure in K- Modes Clustering Algorithm

Dr. Abedalhakeem T. Issa

Computer Science Shaqra University - Dawadmi Community college Computer Science Department Dawadmi 11911 P.O. Box 18 SAUDIA ARABIA

ABSTRACT:

Organizing data into sensible groupings is one of the most fundamental modes of understanding and learning.[1]Clustering is one of the most important data mining techniques that partitions data according to some similarity criterion. The problems of clustering categorical data have attracted much attention from the data mining research community recently [2].The original k-means algorithm [3] or known as Lloyd's algorithm, is designed to work primarily on numeric data sets. This prohibits the algorithm from being applied to definite  data clustering, which is an integral part of data mining and has attracted much attention recently In this paper delineates increase to the k-modes algorithm for clustering definite data. By modifying a simple corresponding Variation measure for definite entities, a heuristic approach was developed in [4, 12], which allows the use of the k-modes paradigm to obtain a cluster with strong intra-similarity, and to efficiently cluster large definite data sets. The main aim of this paper is to derive severely the updating formula of the k-modes clustering algorithm with the new Variation measure, and the convergence of the algorithm under the optimization framework.

KEYWORDS: Data mining; clustering; k-means algorithm; definite data

Copy the following to cite this article: T. Issa A. T. On the Consequence of Variation Measure in K- Modes Clustering Algorithm. Orient.J. Comp. Sci. and Technol;7(3)

Copy the following to cite this URL: T. Issa A. T. On the Consequence of Variation Measure in K- Modes Clustering Algorithm. Orient.J. Comp. Sci. and Technol;7(3). Available from: http://www.computerscijournal.org/?p=1428

Introduction

Advances in sensing and storage technology and dramatic growth in applications such as Internet search, digital imaging, and video surveillance have created many high-volume, and high dimensional data sets [1].

The widespread use of computer and information technology has made extensive data collection in business, manufacturing and medical organizations a routine task. This explosive growth in stored data has generated an urgent need for new techniques that can transform the vast amounts of data into useful knowledge. Data mining is, perhaps, most suitable for this need [5].

Clustering is an important data mining technique that groups together similar data records. The k-modes algorithm [6, 7] has become a popular technique involving definite data clustering problems in different application domains (e.g., [8, 9]). The k-modes algorithm as an extension of the k-means algorithm by using a simple corresponding Variation measure for definite entities, modes instead of means for clusters, and a frequency-based method to update modes in the clustering process to minimize the clustering value function. The goal of data clustering, also known as cluster analysis, is to discover the natural grouping(s) of a set of patterns, points, or objects. Webster (Merriam-Webster Online Dictionary, 2008) [1]. These increases have removed the numeric-only limitation of the k-means algorithm and enable the k-means clustering process to be used to efficiently cluster large definite data sets from real world databases. An equivalent nonparametric approach to deriving clusters from definite data is presented in [10]. A note in [11] discusses the equivalence of the two independently developed k-modes approaches.

The distance between two entities computed with the simple corresponding similarity measures either 0 or 1. This often outputs in clusters with weak intra-similarity. Recently, He et al[4] and San et al. [12] independently introduced a new Variation measure to the k-modes clustering process to enhance the accuracies of the clustering outputs. Their main idea is to use the relative attribute frequencies of the cluster modes in the similarity measure in the k-modes objective function. This modification allows the algorithm to recognize a cluster with weak intra-similarity, and therefore assign less similar entities to such cluster, so that the generated clusters have strong intra-similarities. Experimental outputs in [4] and [12] have shown that the modified k-modes algorithm is profitable.

The aim of this paper is to give a plain proof that the entity cluster membership task method and the mode updating formulae under the new Variation measure indeed minimize the objective function. We also prove that using the new Variation measure the convergence of the clustering process is guaranteed. In [4] and [12], the new Variation measure was introduced heuristically. With the formal proofs, we assure that the modified k-modes algorithm can be used safely.

This paper is organized as follows. In Section 2, we review the k-modes algorithm. In Section 3, we study and analyze the k-modes algorithm with the new similarity measure. In Section 4, examples are given to illustrate the profitability of the k-modes algorithm with the new similarity measure. Finally, a concluding remark is given in Section 5.

by DOM (Su), associated with a defined semantic and a data type. In this paper, we only assume two general data categories, numeric and definite and assume other types used in database systems can be mapped to one of these two types. The domains of attributes associated with these two types are called numeric and definite respectively. A numeric domain consists of real numbers. A domain DOM (Su) is defined as definite if it is countable and unordered, e.g., for any o, pε DOM (Su), either o= por o≠p, see for instance [14].

An object Bin  can be logically represented as a conjunction of attribute-

value pairs [S₁ = B₁] ^∧ [S₂ = B₂] ^∧ ……………………. ^∧ [S_u = B_u] where Bj ε DOM (Sj) for 1≤ j ≤u.

Without ambiguity, we represent Bas a  vector [S₁, S₂……………….S_u]. B is called a definite entity if it has only definite values. We consider every entity has exactly u attribute values. If the value of an attribute _Sj is missing, then we denote the attribute value of S_j by ε.

Let B = (B₁, B₂………._,B_v) be a set of v objects. objects B_d is represented as [ B_d1B_d2…………..,B_du]. We  write B_d = B_e if B_dj = B_ej 1≤ j≤u. The relation B_d = B_e does not mean that B_d and Be are the same entity in the real world database, but rather that the two entities have equal values in attributes S₁, S₂,………………S_u.

The k-modes algorithm, introduced and developed in [6, 7], has made the following modifications to the k-means algorithm: (i) using a simple corresponding Variation measure for definite entities, (ii) replacing the means of clusters with the modes, and (iii) using a frequency based method to find the modes. These modifications have removed the numeric-only limitation of the k-means algorithm but maintain its efficiency in clustering large definite data sets [7].

Let Band C be two definite objects represented by [B₁, B_2,…………B_u] and [C_1, C₂………….C_u] respectively. The simple matching Variation  measure between Band C is defined as follows:

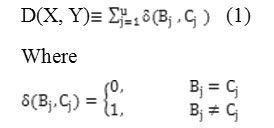
It is easy to verify that the function d defines a metric space on the collection of definite entities. Traditionally, the simple corresponding approach is often used in binary variables which are converted from definite variables ([3], pp.28-29). We note that D is also a kind of generalized.

Hamming Distance

Hamming is the percentage of bits that differ, it is suitable for binary data only. Each centroid is the component-wise median of points in that cluster. The k-modes algorithm uses the k-means paradigm to cluster definite data. The objective of clustering a set of definite objects into k clusters is to find Rand that minimize

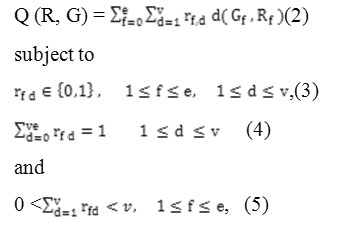
Whereof (≤ v) is a known number of clusters, R= [r_fd] is is a k-by-v{0, 1}matrix, G = [G₁, G₂], and G_d is the d^th  cluster center with the definite  attributes S₁,S_{2 ……………………………,}S_u.

Minimization of Qin (2) with the constraints in (3), (4) and (5) forms a class of constrained nonlinear optimization problems whose solutions are unknown. The usual method towards optimization of Qin (2) is to use partial optimization for Grand R. In this method we first fix and find necessary conditions on R to minimize Q. Then we fix R and minimize Q with respect to G. This process is formalized in the k-modes algorithm as follows.

Algorithm The K-Modes Algorithm

Solution Approach by k-Modes Algorithm

1.  Choose an initial point G⁽¹⁾ ε IH^ue, Determine R⁽¹⁾ such that Q (R, G⁽¹⁾) is minimized. Set x= 1.
2. Determine R⁽¹⁾ such that Q (R^x,G^(X+1) ) is minimized. If Q  (R^x,G^(X+1) ) Q (R^x, G^x) then stop; otherwise go to step 3.
3. Determine R^x+1 such that Q (R^(x+1), G ^(x+1)) is minimized.
4. If Q (R^(x+1),G R^(x), G^(x+1)), then stop; otherwise set x=x+ 1 and go to Step 2.

5. The matrices Rand G are calculated according to the following two theorems.Theorem 1: Let 12G”>  be fixed and consider the problem.

6. min_r Q (R, G) Subject to (3), (4) and (5) The minimize 12R”> is given by.

 

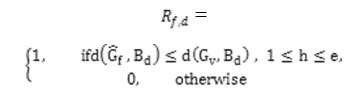
Theorem 2: Let B be a set of definite entities delineates by definite attributes S₁,S₂ ………,….. S_u and DOM (S_j) = {s_j^(1), s_j ^{(2),………………,………..}s^_jvj} where v_j is the number of categories of attribute ≤ j ≥ u. Let the cluster centers G_f be represented by [ G_{f ,1,} G_{f, m}] for ≤ f ≥. Then the quantity Σ ^e_{f =} Σ^v_{d =} r_1,1D (G_f,B_d) is minimized if G_{fj =} S_j^(y) ε DOM (S_j) where 

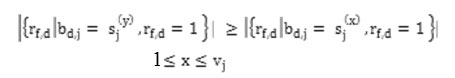
For 1≤j≤u. Here |B| denotes the number of elements in the set B.

We remark that the minimum solution r^∧ is not unique, so r_f,_d= 

1 may arbitrarily be assigned to the first minimizing index f, and the remaining entries of this column are put to zero. This problem occurs frequently when clusters have weak intra-similarities, i.e., the attribute modes do not have high frequencies.

Let us consider the following example to demonstrate the problem using the simple matching Variation. The data set is described with three definite  attributes s₁ (2 categories: 1 or2), S_2 (2 categories: 1 or 2) and S₂ (5 categories: 1, 2, 3, 4 or 5) and there are two clusters with their modes and their three objects:

 

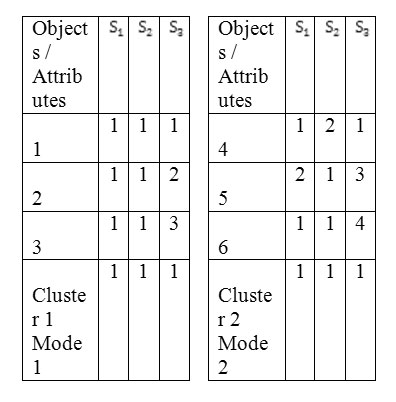
The above example shows that the similarity measure does not represent the real semantic distance between the objects and the cluster mode. For example, if an object B= [1 1 5]is assigned to one of the clusters, then we find that D ( , B) = 1 = D ( , B). Therefore we cannot determine the assignment of B properly.

The New Variation Measure
He et al. [12] and San et al. [4] independently introduced a Variation measure in the k-modes objective function. More precisely, they minimize.

Q_v (R; G) = Σ ^e_{f = 1} Σ ^v_d:

Subject to the conditions same as in (3), (4) and (5). The Variation measured_v (G_f, B_d) is defined as follows:

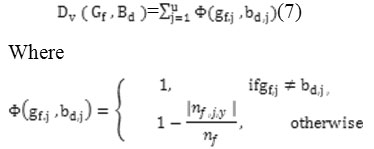
where | n_f| is the number of objects in f^th the cluster, given by

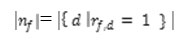
And |n_{f, jy}| is the number of objects with category S_j^(y) of the j^th attribute in the f^th cluster, given by 

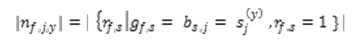
According to the definition of φ the dominant level of the mode category is considered in the calculation of the Variation measure. When the mode category is 100% dominant, we have |n_f| = |n_{f, jy}| and therefore the corresponding function value is the same as in (1) in the original k-modes algorithm.

Let us consider the example in Section 2 again; the computed parameters |n_{f, jy}| are given as follows

 

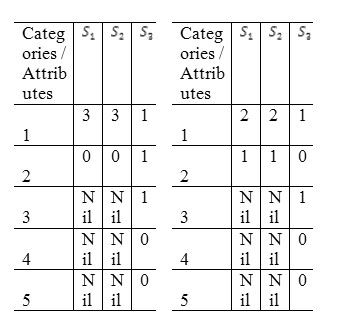
Now if an object B= [1 1 5] is assigned to one of the clusters, the new Variation  measure can represent the real semantic distance, we have D_v (N_1, B) = 1 and D_v (N₂, B) =5/3. The object B is assigned to the first cluster properly.

Now the key issue is to derive severely the updating formula of the k-modes clustering algorithm with the new Variation measure, similar to Theorem 2. In [4, 12], the authors presented heuristically the updating formula only using the k-modes framework. We remark that the matrix R can be calculated according to Theorem 1. Theorem 3 below show severely the updating formula of Gin the k-modes clustering algorithm with the new Variation measure.

Theorem 3 Let B be a set of definite  objects described by definite  attributes,S_{2, ………………….,} S_{u  12Su”>} and DOM (Sj)

{s_j^(1), s^{_{j(2),………………. …. ..,}}s_j^(vj)}, where v_j is the number of categories of attribute S_j for 1 ≤ j ≥ u. Let  the cluster centers G_f be represented by [G_f,1, G_{f,2, …… …… …….,} G_f,u] for 1 ≤ f ≥ u. Then the quantity Σ ^e_{f =} Σ^v_{d =1} ^r_{f,d^{Dv (Gf, Bd)}} is minimized if  G^_f,d = S_j^(y) ε DOM (S_j) 

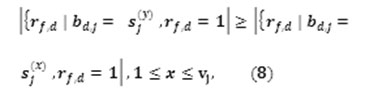
for  ≤ j ≥ u.

Proof: For a given R, all the inner sums of the quantity.

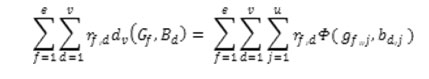
are nonnegative and independent. Minimizing the quantity is equivalent to minimizing each inner sum. We write the (f,j)^th inner sum (1≤ f ≥  and 1 ≤ j ≥ u) as.

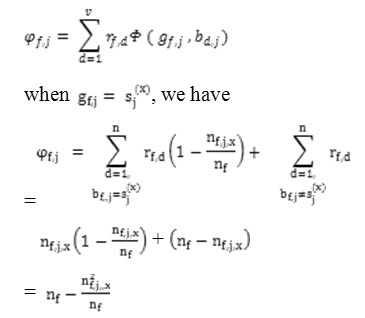
It is clear that φ_f,j is minimized if n_{f, j,x} is maximal for 1≤ x ≥ v_j. Thus the term |{r_f,d|b_d,j = g_f,j, r_f,d =1| must be maximal. The result follows. According to (8), the category of attribute S_j of the cluster mode G_f  is determined by the mode of categories of attribute S_j in the set of objects belonging to cluster f.

By comparing the results in Theorems 2 and 3, the cluster centers are updated in the same manner even we use different distance functions in (1) and (7) respectively. It implies that the same k-mode algorithm can be used. The only difference is that we need to count and store |n_{f, j,y}| and |n_f| in each iteration for the distance function evaluation.

Combining Theorems 1 and 3 with the algorithm forms the k-modes algorithm with the new Variation measure, in which the modes of clusters in each iteration are updated according to Theorem 3 and the partition matrix is computed according to Theorem 1. We remark that the updating formulae of Rand Gin Theorems 1 and 3 respectively are determined by solving two minimization sub problems from (2):

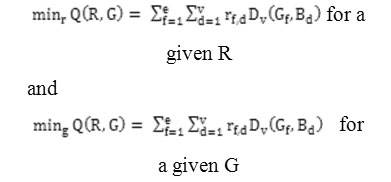
The convergence of the k-modes algorithm with the new Variation measure can be obtained as in Theorem 4 below.

Theorem 4 the k-modes algorithm with the new Variation measure converges in a finite number of iterations.

Proof: We first note that there are only a finite number (M = π ^u_{j = 1} ^v_j) of possible cluster centers (modes). We then show that each possible centre appears at most once by the k-modes algorithm. Assume that G^{(x₁) =} G^(x₂) where x_1 ≠ x_2.

According to the k-modes algorithm we can compute the minimizes R^(x₁) and R^(x₁) for G = G^(x₁) and G = G^(x₂) respectively.

Therefore, we have 

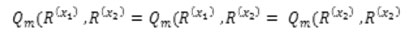
However, the sequence Q_m (.   ,    .) generated by the k-modes algorithm with the new Variation measure is strictly decreasing. Hence the result follows.

The result of Theorem 4 guarantees the decrease of the objective function values with respect the iterations of the k-modes algorithm with the new Variation measure.

Experimental Results

A comprehensive performance study has been conducted to evaluate our method. In this section, we delineate those experiments and their results. In [4, 12], experimental outputs are given to illustrate that the k-mode algorithm with the new Variation measure performs better in clustering accuracy than the original k-mode algorithm. The main aim of this section is to illustrate the convergence output and evaluate the clustering performance and efficiency of the k-mode algorithm with the new Variation measure. We will use a soybean dataset obtained from the UCI Machine Learning Repository [13] to generate several examples to test the k-modes algorithm with the new Variation measure. The soybean dataset includes 47 records, each of which is described by 35 attributes. It is an experimental comparison of the two methods of knowledge acquisition in the context of developing an expert system for soybean disease diagnoses. Each record is labeled as one of the4 diseases: L1, L2, L3 and L4. Except for L4 which has 17 instances, all other diseases only have 10 instances each. We only selected 21 attributes in these experiments, because the other attributes only have one category. We carried out 100 runs of the k-mode algorithm with the new Variation measure and the original k-mode algorithm on the data set. In each run, the same initial cluster centers were used in both algorithms. In Figure 1, we show the 100 curves, where each curve refers to the objective function values with the iterations of the k-mode algorithm using the new Variation measure. It is clear from the figure that the objective function values are decreasing in each curve. With our results in Theorem 3, we show that the objective function values are decreasing when the new similarity measure is used. We also see Figure 1 that the algorithm stops after 

Table1: The summary results for 100 runs of two algorithms on the soybean data set.   Click here to View table

 

Finite number of iterations, i.e., the objective function values does not decrease any more. This is exactly the results we showed in Theorem 4. The k-modes algorithm with the new Variation measure can be used safely.

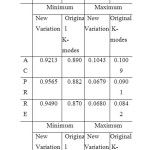
To evaluate the performance of clustering algorithms, we consider three measures: (i) accuracy (AC), (ii) precision (PE) and (iii) recall (RE). Objects in a f^th cluster are assumed to be classified either correctly or incorrectly with respect to a given class of objects. Let the number of correctly classified objects be s_f, let the number of incorrectly classified objects be n_f and let the number of objects in a given class but not being in a cluster be n_f  clustering accuracy, recall and precision are defined as follows: 

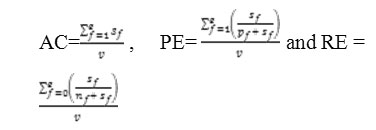
Respectively Table 1 shows the summary results for both algorithms. According to Table 1,the performance of the k-mode algorithm with the new similarity measure is better than the original k-mode algorithm for AC, PE and RE.

Next we test the scalability of the k-mode algorithm with the new Variation measure. Synthetic definite data sets are generated by the method in [7] to evaluate the algorithm. The number of clusters, attributes and categories of synthetic data is ranged in between 3 to 24.The number of objects is ranged in between 10,000 and 80,000. The computational results are performed by using a machine with an Apple iBook G4 and 1Gega RAM. The computational times of both algorithms are plotted with respect to the number of clusters, attributes, categories and objects, while the other corresponding parameters are fixed.

The k-mode algorithm with the new similarity measure requires more computational times than the original k-mode algorithm. It is an expected outcome since the calculation of the new Variation measure requires some additional arithmetic operations. However, according to the tests, the k-mode algorithm with the new Variation measure is still scalable, i.e., it can cluster definite objects efficiently.

Conclusion

In this paper, we state extremely rules the updating formula of the k-modes clustering algorithm with the new Variation measure, and the convergence of the algorithm under the optimization structure. Experimental results show that the k-mode algorithm with the new Variation measure is adequate and effective in clustering definite data sets.

References

1. Fuyuan Cao, Jiye Liang, Deyu Li, Liang Bai, Chuangyin Dang\ “A Dissimilarity Measure for the K-Modes Clustering Algorithm” , ELSEVIER, Knowledge-Based Systems 26 (2012) 120–127 .
   CrossRef
2. Anil K. Jain\ ” Pattern Recognition Letters” , ELSEVIER, Pattern Recognition Letters 31 (2010) 651–666 .
3. A. K. Jain and R. C. Dubes, Algorithms for Clustering Data. Englewood Cliffs, NJ: Prentice Hall, 1988.
4. B. Andreopoulos, A. An and X.Wang \Clustering the Internet Topology at Multiple Layers,” WSEAS Transactions on Information Science and Applications, Vol. 2, No. 10, Pp. 1625-1634, 2005.
5. J. Han, M. Kamber, Data Mining Concepts and Techniques, Morgan Kaufman, San Francisco, 2001.
6. A. Chaturvedi, P. Green and J. Carroll \K-Modes Clustering,” Journal of Classification, Vol. 18, Pp. 35{55, 2001.12
   CrossRef
7. K. C. Gowda And E. Diday, \Symbolic Clustering Using A New Dissimilarity Measure”, Pattern Recognition, Vol. 24, No. 6, Pp. 567-578, 1991.
8. Z. Huang \A Fast Clustering Algorithm to Cluster Very Large Categorical Data Sets in Data Mining,” in Proceedings of the SIGMOD Workshop on Research Issues on Data Mining and Know Ledge Discovery, Tucson, Arizona, USA, Pp. 1{8, 1997.
9. L. Kaufman and P. J. Rousseeuw, Finding Groups in Data – An Introduction to Cluster Analysis. Wiley, 1990.
10. Z. Huang, \Extensions to the K-Means Algorithm for Clustering Large Data Sets with Categorical Values”, Data Mining and Knowledge Discovery, Vol. 2, No. 3, Pp. 283-304, 1998.
11. Z. Huang and M. Ng, \A Note on K-Modes Clustering”, Journal of Classification, Vol. 20, Pp. 257{261, 2003}.
12. Yiling Yang, Xudong Guan, Jinyuan You/ ” A Fast And Effective Clustering Algorithm For Transactional Data”, KDD ’02 Proceedings Of The Eighth ACM SIGKDD International cConference on Knowledge Discovery and Data Mining Pages 682-687.
13. Ryan Rifkin, Aldebaro Klautau, “in Defense of One-Vs-All Classification”, the Journal of Machine Learning Research, Volume 5, 12/1/2004 Pages 101-14.
14. Z. Huang and Michael Ng, \A Fuzzy K-Mode Algorithm for Clustering Categorical Data”, IEEE Transactions on Fuzzy System, Vol. 7, No. 4, 1999
15. Z. He, S. Deng And X. Xu, \Improving K-Modes Algorithm Considering Frequencies of Attribute Values in Mode”, International Conference on Computational Intelligence and Security, LNAI 3801, Pp. 157{162, 2005

---

This work is licensed under a Creative Commons Attribution 4.0 International License.