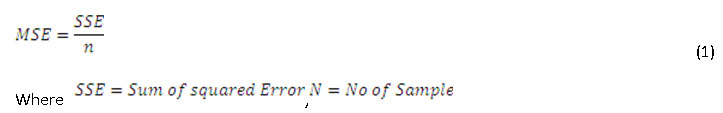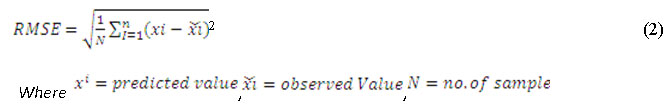Comparision Between Accuracy and MSE,RMSE by Using Proposed Method with Imputation Technique

V.B. Kamble^1* and S.N. Deshmukh²

¹P.E.S. College of Engineering, Aurangabad. (M.S.) India.

²Dr. Babasaheb Ambedkar Marathwada University, Aurangabad. (M.S.), India.

Corresponding author Email: Vbkamble@yahoo.com

DOI : http://dx.doi.org/10.13005/ojcst/10.04.11

ABSTRACT:

Presence of missing values in the dataset leads to difficult for data analysis in data mining task. In this research work, student dataset is taken contains marks of four different subjects in engineering college. Mean, Mode, Median Imputation were used to deal with challenges of incomplete data. By using MSE and RMSE on dataset using with proposed Method and imputation methods like Mean, Mode, and Median Imputation on the dataset and found out to be values of Mean Squared Error and Root Mean Squared Error for the dataset. Accuracy also found out to be using Proposed Method with Imputation Technique. Experimental observation it was found that, MSE and RMSE gradually decreases when size of the databases is gradually increases by using proposed Method. Also MSE and RMSE gradually increase when size of the databases is gradually increases by using simple imputation technique. Accuracy is also increases with increases size of the databases.

KEYWORDS: Incomplete data; Missing Values; Imputation; Mean Imputation; Median Imputation and Mode Imputation; MSE(Mean Squared Error); RMSE(Root Mean Squared Error )etc

Copy the following to cite this article: Kamble V. B, Deshmukh S. N. Comparision Between Accuracy and MSE,RMSE by Using Proposed Method with Imputation Technique. Orient.J. Comp. Sci. and Technol;10(4)

Copy the following to cite this URL: Kamble V. B, Deshmukh S. N. Comparision Between Accuracy and MSE,RMSE by Using Proposed Method with Imputation Technique. Orient. J. Comp. Sci. and Technol;10(4). Available from: http://www.computerscijournal.org/?p=7140

Introduction

Missing data imputation techniques can be used to improve the data quality. Missing data imputation techniques replace missing values of a dataset so that data analysis methods can be applied to complete dataset.¹

In this research work, student dataset is taken contains marks of four different subjects in engineering college. Mean, Mode, Median Imputation were used to deal with challenges of incomplete data. By using MSE and RMSE on dataset using with proposed Method and imputation methods like Mean, Mode, and Median Imputation on the dataset and found out to be values of Mean Squared Error and Root Mean Squared Error for the dataset. Accuracy also found out to be using Proposed Method with Imputation Technique. Experimental observation it was found that, MSE and RMSE gradually decreases when size of the databases is gradually increases by using proposed Method. Also MSE and RMSE gradually increase when size of the databases is gradually increases by using simple imputation technique. Accuracy is also increases with increases size of the databases.

The organization of the paper is Section1: Introduction Section 2: Literature Reviews, Section 3: Dataset Used, Section 4: Methodology, Section 5:Experimental Result and Analysis, Section 6: Conclusions

Literature Reviews

Lit Wise Deletion

This method deletes those instances with missing value for data analysis in the dataset. It is the most common method, it has two drawbacks: a) A substantially decreases the size of dataset available for the data analysis. b) Data are not always missing completely at random.

Mean/Mode Imputation (MMI)

By replacing a missing values with the mean or mode of all attribute which consists missing value. To reduce the influence of exceptional data, median can also be used. This is one of the most commonly used methods.

K-Nearest Neighbor Imputation (KNN)

This method uses k-nearest neighbor algorithms to estimate and replace missing data. The main advantages of this method are a) it can estimate both qualitative attributes and quantitative attributes; b) It is not necessary to build a predictive model for each attribute with missing data.²

Median Substitution

Median Substitution is calculated by grouping up of data and finding average for the data. Median can be calculated by using the formula

Median =L+h/f (n/2-c)                                                                                  (1)

where L is the lower class boundary of median class h is the size of median class i.e. difference between upper and lower class boundaries of median class f is the frequency of median class, c is previous cumulative frequency of the median class, n/2 is total no. of observations divided by 2

Standard Deviation

The standard deviation measures the spread of the data about the mean value. It is useful in comparing sets of data which may have the same mean but a different range. The Standard Deviation is given by the formula

Where{X1,X2,…,X­­_n}are the observed values of the sample items and is the mean value of these observations, while the denominator N stands for the size of the sample.⁷

Dataset Used

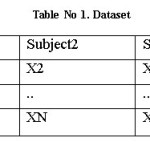
In this work dataset having characteristics is given below.

Number of Instances: 5000,10,000,15,000,20,000

Number of Attributes: 05

(Record No., M1, ECE, EM, EE)

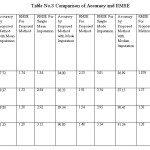
Dataset contains marks of four different subjects of engineering college. In dataset randomly distributed the missing values in each attribute to become the incomplete dataset. Record. No. in the Dataset is used are imaginary and generated for the data analysis purpose in data mining process. In dataset M1, ECE, EM, EE are the subject in engineering college and class test marks for each subject is out of twenty marks for each subject respectively. The structure of Dataset as shown in the Table No.1

Table 1: Dataset  Click here to View table

 

Methodology

To found out accuracy by using proposed method with imputation technique like mean, mode and median for five thousand dataset, ten thousand dataset, fifteen thousand dataset and twenty thousand dataset.    

To found out MSE (Mean Squared Error) for proposed method with mean imputation technique and simple mean imputation technique by using following equation

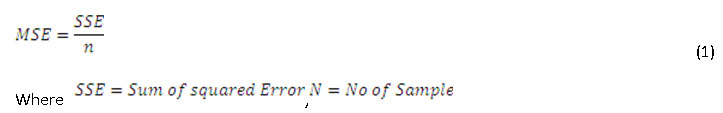
To found out MSE (Mean Squared Error) for proposed method with mode imputation technique and simple mode imputation technique by using equation no.1.     

To found out MSE (Mean Squared Error) for proposed method with median imputation technique and simple median imputation technique by using equation no.1.

To found out RMSE (Root Mean Squared Error) for proposed method with mean imputation technique and simple mean imputation technique by using following equation

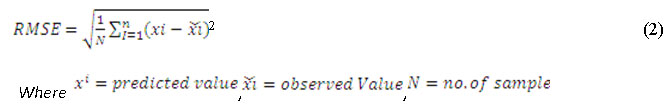
To found out RMSE (Root Mean Squared Error) for proposed method with mode imputation technique and simple mode imputation technique by using equation no.2

To found out RMSE (Root Mean Squared Error) for proposed method with median imputation technique and simple median imputation technique by using equation no.2

Experimental Result and Analysis

For Experimental Result Student dataset is taken which contains marks of four different subjects of engineering college. Mean, Mode, Median Imputation were used to deal with challenges of incomplete data.

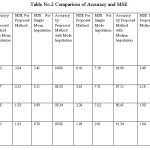
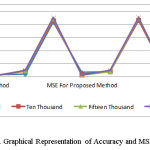
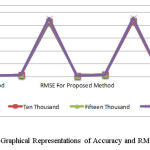
Using proposed method with imputation techniques like Mean, Mode, and Median Imputation on the student dataset and found out to be accuracy for five thousand, ten thousand, fifteen thousand and twenty thousand dataset respectively. Accuracy increase with increase in size of the dataset.      

Similarly found out to be MSE by using Proposed Method with Imputation Technique like Mean, Mode, and Median Imputation. MSE decreases with increase in size of the dataset.

Found out to be MSE by using simple Imputation Technique like Mean, Mode, and Median Imputation. MSE increase with increase in size of the dataset.      

Similarly found out to be RMSE by using Proposed Method with Imputation Technique like Mean, Mode, and Median Imputation. RMSE decreases with increase in size of the dataset.

Also found out to be RMSE by using simple Imputation Technique like Mean, Mode, and Median Imputation. RMSE increase with increase in size of the dataset.

Accuracy found out to be by proposed method with Imputation Technique like Mean, Mode, and Median Imputation. Also MSE by using Proposed Method with Imputation Technique and MSE by using simple Imputation Technique, RMSE by using Proposed Method with Imputation Technique, RMSE by using simple Imputation Technique. The result is shown in the Table no.2 and Table no.

Table 2: Comparison of Accuracy and MSE  Click here to View table

 

Figure 1: Graphical Representation of Accuracy and MSE  Click here to View figure

 

Table 3: Comparison of Accuracy and RMSE  Click here to View table

 

Figure 2: Graphical Representations of Accuracy and RMSE  Click here to View figure

 

Conclusions

In this research paper by using proposed method with imputation technique like Mean, Mode and Median Imputation on the student dataset and found out to be accuracy. Also found out to be MSE and RMSE on dataset using with proposed Method and imputation methods like Mean, Mode, and Median Imputation on the dataset. Experimental observation it is found that, MSE and RMSE gradually decreases when size of the databases is gradually increases by using proposed Method. Also MSE and RMSE gradually increase when size of the databases is gradually increases by using simple imputation technique. Accuracy increase with increase in size of the dataset.

Acknowledgment

I wishes to thank my guide and Data Analytics Laboratory of Department of Computer Science and Information Technology, Dr. Babasaheb Ambedkar Marathwada University, Aurangabad.

References

1. Dinesh J. Prajapati, Jagruti H. Prajapati, “Handling Missing Values: Application to University Data set”. Issue 1, Vol. 1(August-2011), ISSN 2249-6149
2. Shamsher Singh, Prof. Jagdish Prasad, “Estimation of Missing Values in the Data Mining and comparison of Imputation Methods”. Mathematical Journal of Interdisciplinary Sciences.2013;1(1):75–90.
   CrossRef
3. Xiao Feng Zhu, Shichao Zhang, Senior Member, IEEE, Zhi Jin, Senior Member, IEEE, Zili Zhang, and Zhuoming Xu, “Missing Value Estimation for Mixed-Attribute Data Sets”. IEEE Transactions on Knowledge And Data Engineering. 2011;23:(1).
4. T.R.Sivapriya, V. Thavavel, A.R.Nadira Banu Kamal, “Imputation and classification of Missing Data Using Least Square Support Vector Machines, A New Approach in Dementia Diagnosis”, International Journal of Advanced Research in Artificial Intelligence.2012;1(4)
5. Yann-Yann Shieh, “Imputation Methods on General Linear Mixed Models of Longitudinal Studies”, American Institutes for Research.
6. Edgar AcuNa And Caroline Rodriguez, “The Treatment Of Missing Values And Its Effect In The Classifier Accuracy Studies In Classification”, Data Analysis, And Knowledge Organization. Springer. Com. 2004.
7. MS. R. Malarvizhi, Dr. Antony Thanamani, “Comparision of Imputation Techniques after Classifying the Dataset Using KNN Classifier for the Imputation of Missing Data”. International Journal of Computational Engineering Research (IJCER online.com) ISSN.2013;2250-3005.
8. Anjana Sharma, Naina Mehta, Iti Sharma, “Reasoning With Missing Values in Multi Attribute Datasets”. International Journal of Advanced Research in Computer Science and Software Engineering.2013;3(5):ISSN: 2277 128X
9. Luai Al Shalabi, “A comparative study of techniques to deal with missing data in data sets”, In Proceedings of the 4^th International Multiconference on Computer Science and Information Technology CSIT.2006.
10. A. Pujari, “Data Mining Techniques”, Universities Press, India. 2001.
11. Ragel, A. and Cremilleux, B., “MVC A pre-processing method to deal with missing values”. In Proceedings of Knowledge Based Systems.1999;285-291.
12. Chih-Hung Wu, Chian-Huei Wun, Hung-Ju Chou, “Using Association Rules for Completing Missing Data”, Fourth International Conference on Hybrid Intelligent Systems (HIS’04). 2004;236-241.
13. Lakshminarayan K., Harp S., Goldman, R. and Samad, “Imputation of missing data using machine learning techniques, In Proceedings of the Second International Conference on Knowledge Discovery in Databases and Data Mining. T. 1996.
14. Zhang, S.C., “Information Enhancement for Data Mining”, IEEE Intelligent Systems.2004;19(2):12-13..
15. Qin, Y.S.,“Semi-parametric Optimization for Missing Data Imputation”. Applied Intelligence 2007;27(1):79-88.  
    CrossRef
16. Zhang, C.Q.,” An Imputation Method for Missing Values”, PAKDD, LNAI, 4426. 2007;1080-1087.
    CrossRef
17. Han J. and Kamber M., “Data Mining: Concepts and Techniques”, Morgan Kaufmann Publishers, 2nd edition. 2006.
18. A. Dempster, N.M. Laird and D. Rubin, “Maximum Likelihood from Incomplete Data via the EM Algorithm”, J. Royal Statistical Soc. 1977;39:1-38.
19. R. Little and D. Rubin, “Statistical Analysis with Missing Data”, second ed. John Wiley and Sons. 2002.
    CrossRef
20. D. Rubin, “Multiple Imputations for Non responsive in Surveys”, Wiley. 1987.
    CrossRef
21. J.R. Quinlan, “C4.5: Programs for Machine Learning”. Morgan Kaufmann. 1993.
22. Q.H. Wang and R. Rao, “Empirical Likelihood-Based Inference under Imputation for Missing Response Data”, Annals of Statistics.2002;30:896-924.
    CrossRef
23. S.C. Zhang, “Par imputation: From Imputation and Null-Imputation to Partially Imputation”, IEEE Intelligent Informatics Bull.2008;9(1):32-38.
24. V.B. Kamble, S.N. Deshmukh, “Comparison of Percentage Error by using Imputation Method On Mid Term Examination Data”. International Journal of Innovations in Engineering Research and Technology (IJIERT),Impact Factor 2.77. 2015;2(12)
25. V.B. Kamble, S.N. Deshmukh,”Comparative Analysis Of Standard Error Using Imputation Method”, ICITDCEME’15 Conference Proceedings on International Conference on Innovations and Technological Developments in Computer, Electronics and Mechanical Engineering.28-29, December 2015, VACOE Ahmednagar. ISSN N0. 2394-3696
26. V.B. amble, S.N. Deshmukh,”A Novel Hybrid Approach for Prediction of Missing Values In Numeric Dataset” Global Journal of Engineering Science and Research Management, Impact Factor: 2.265, ISSN 2349-4506.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.