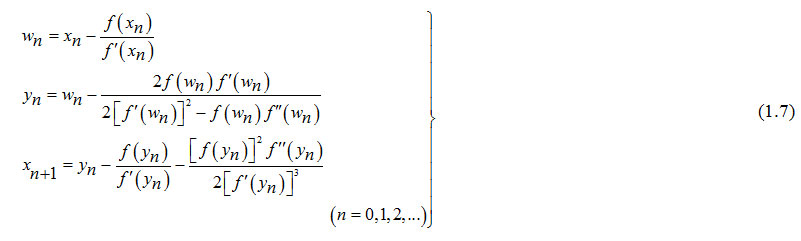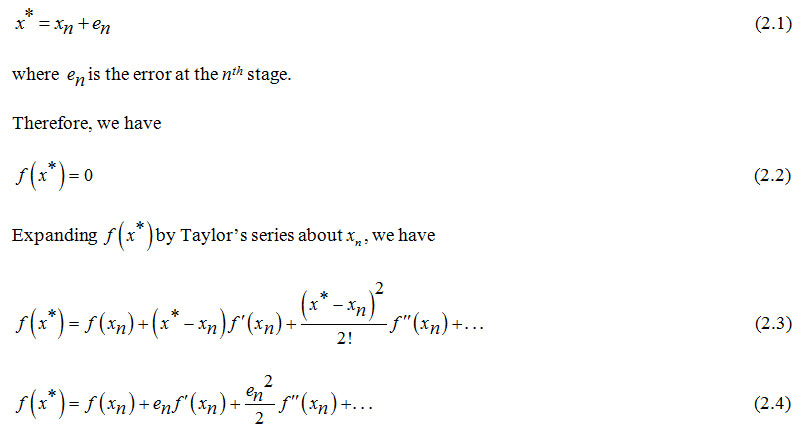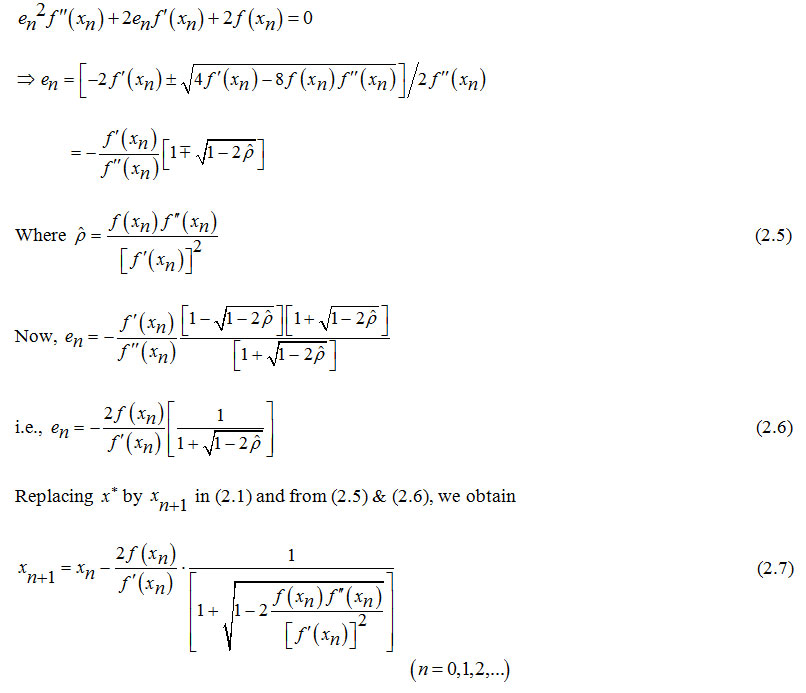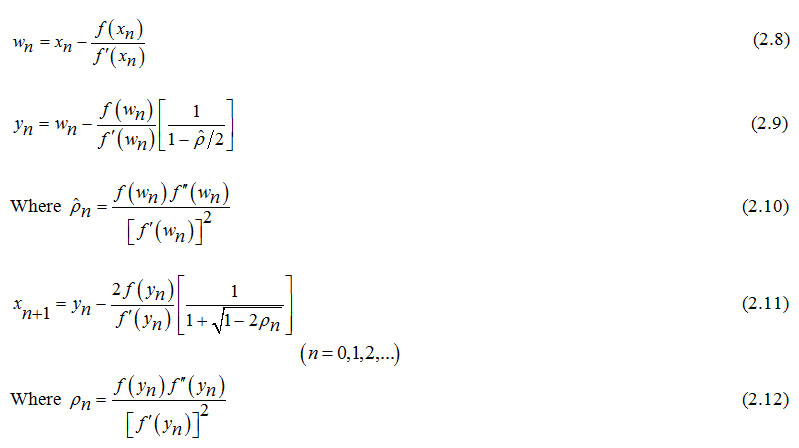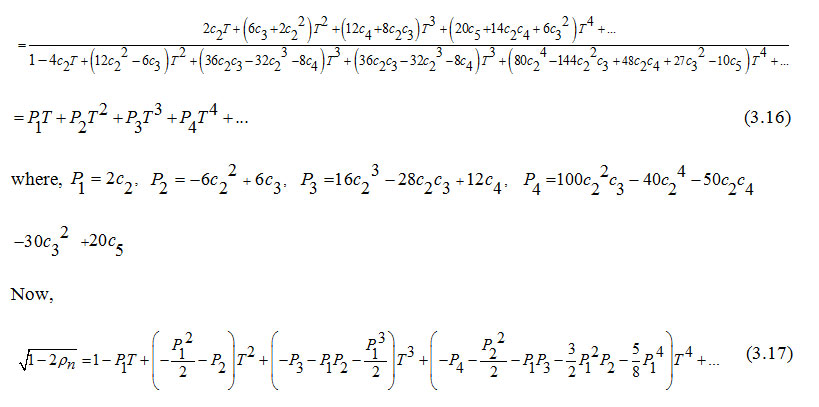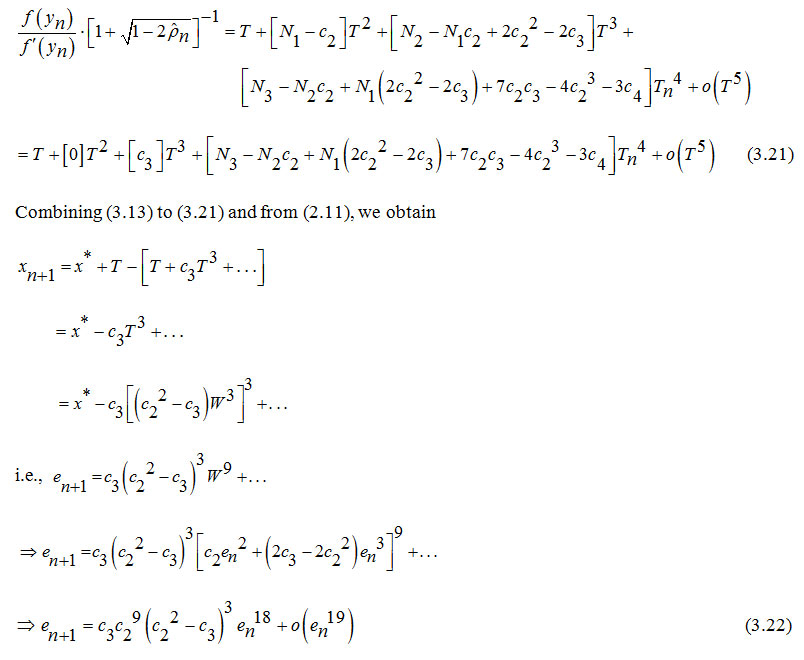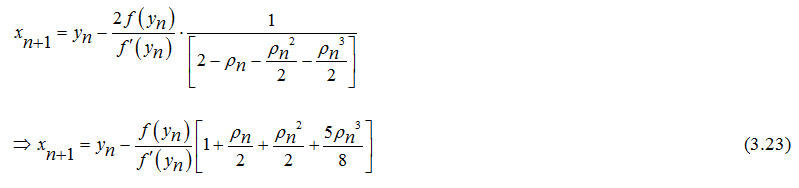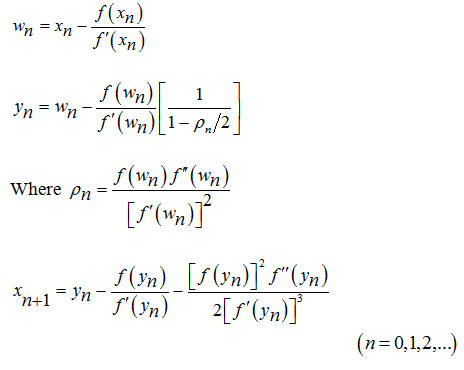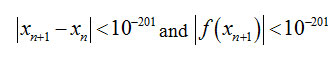Eighteenth Order Convergent Method for Solving Non-Linear Equations

V.B. Kumar Vatti¹, Ramadevi Sri¹ and  M.S. Kumar Mylapalli²

¹Dept. of Engineering Mathematics, Andhra University, Visakhapatnam, India

³Dept. of Engineering Mathematics, Gitam University, Visakhapatnam, India

 

Corresponding author Email: drvattivbk@yahoo.co.in

DOI : http://dx.doi.org/10.13005/ojcst/10.01.19

ABSTRACT:

In this paper, we suggest and discuss an iterative method for solving nonlinear equations of the type f(x)=0  having eighteenth order convergence. This new technique based on Newton’s method and extrapolated Newton’s method. This method is compared with the existing ones through some numerical examples to exhibit its superiority.

AMS Subject Classification:  41A25, 65K05, 65H05.

KEYWORDS: Iterative method; Nonlinear equation; Newton’s method; Convergence analysis; Higher order convergence

Copy the following to cite this article: Vatti V. B. K, Sri R, Mylapalli M. S. K. Eighteenth Order Convergent Method for Solving Non-Linear Equations. Orient.J. Comp. Sci. and Technol;10(1)

Copy the following to cite this URL: Vatti V. B. K, Sri R, Mylapalli M. S. K. Eighteenth Order Convergent Method for Solving Non-Linear Equations. Orient.J. Comp. Sci. and Technol;10(1). Available from: http://www.computerscijournal.org/?p=4905

Introduction

We consider finding the zero’s of a nonlinear equation

f(x)=0          (1)

Where f: D c R→R is a scalar function on an open interval D and f(x) may be algebraic, transcendental or combined of both. The most widely used algorithm for solving (1.1) by the use of value of the function and its derivative is the well known quadratic convergent Newton’s method (NM) given by

starting with an initial guess x₀ which is in the vicinity of the exact root x*. The efficiency index of Newton’s method is 2√2 = 1.4142. The Extrapolated Newton’s method (ENM) suggested by V.B.Kumar, Vatti et.al [11] which is developed by extrapolating Newton’s method (1.2) introducing a parameter ‘α_n‘ given by.

 

Which is same as Halley’s method having third order convergence requires three functional evaluations. The efficiency index of this method is 3√3=1.4422.

A three step Predictor-corrector Newton’s Halley method (PCNH) suggested by Mohammed and Hafiz [10] (see[1to10]), is given by:

For a given  x_0, we compute x_n+1 by using.

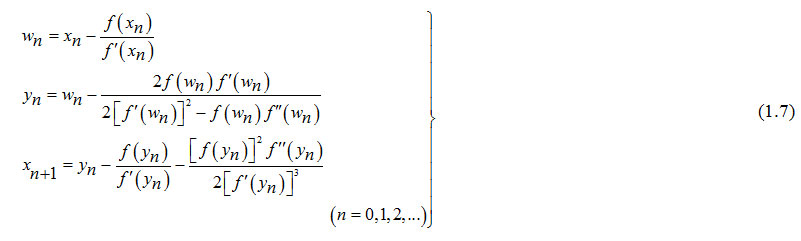
This method has eighteenth order convergence and its efficiency index is 8√18=1.4352.

In section 2, we develop and discuss a three step iterative method and the convergence criteria is discussed in section 3. Few numerical examples are considered to show the superiority of this method in the concluding section.

Eighteenth Order Convergent Method (Eocm)

Consider x* be the exact root of (1.1) in an open interval D in which f(x) is continuous and has well defined first and second derivatives. Let x_n be the n^th approximate to the exact root x* of (1.1) and. 

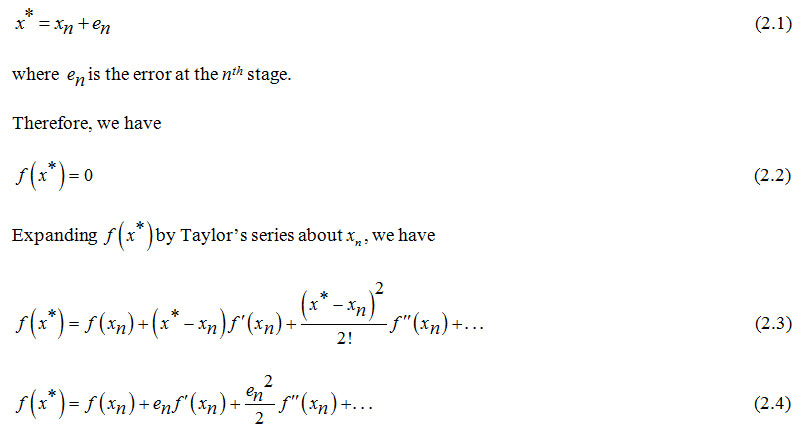
Assuming e_n is small enough and neglecting higher powers of e_n starting from onwards, we obtain from (2.2) and (2.4) as

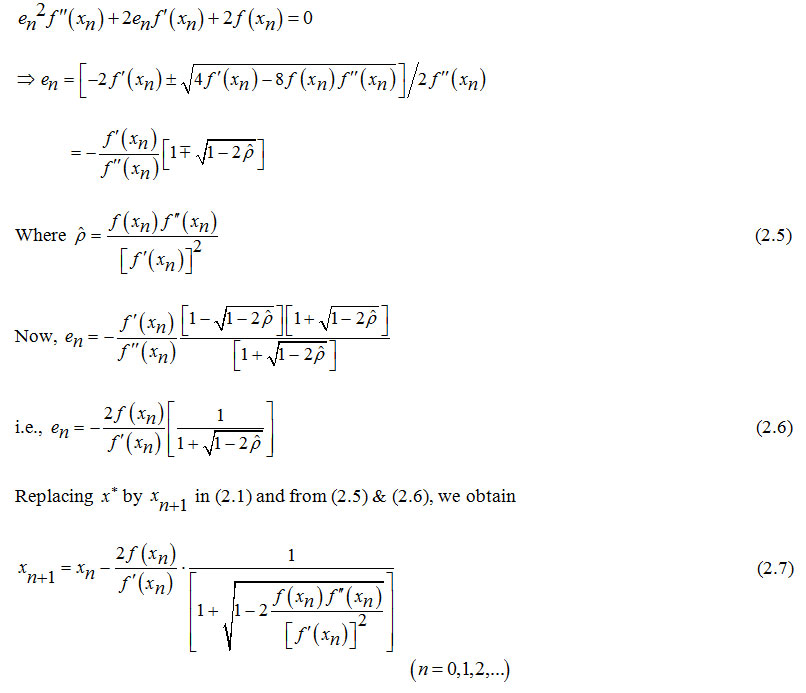
This scheme (2.7) allows us to propose the following algorithm with the method (1.2) as the first step and the method (1.6) as the second step.

Algorithm 2.1:  For a given x₀, compute x_n+1 by the iterative schemes.

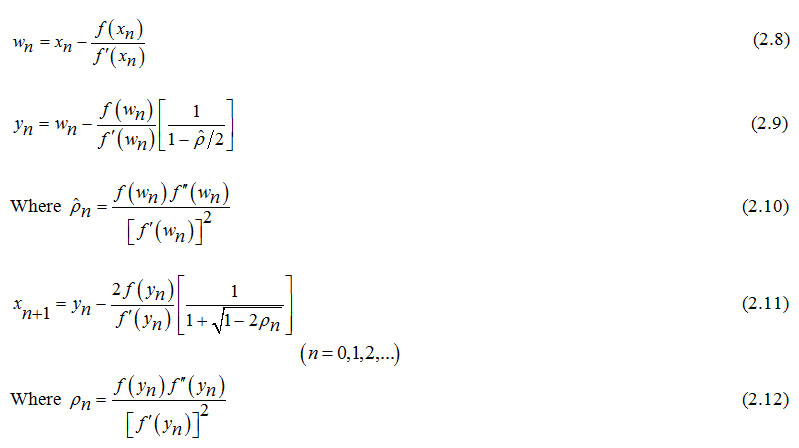
This algorithm (2.1) requires 3 functional evaluations, 3 of its first derivatives and 2 of its second derivatives and can be called as Eighteenth order Convergent Method (EOCM).

Convergence Criteria

Theorem 3.1.Let x*∈D be a single zero of a sufficiently differentiable function f: D⊂R→R for an open interval D. If x₀ is in the vicinity of x*, then the algorithm (2.1) has eighteenth order convergence.

Proof: Let x* be a single zero of (1.1) and

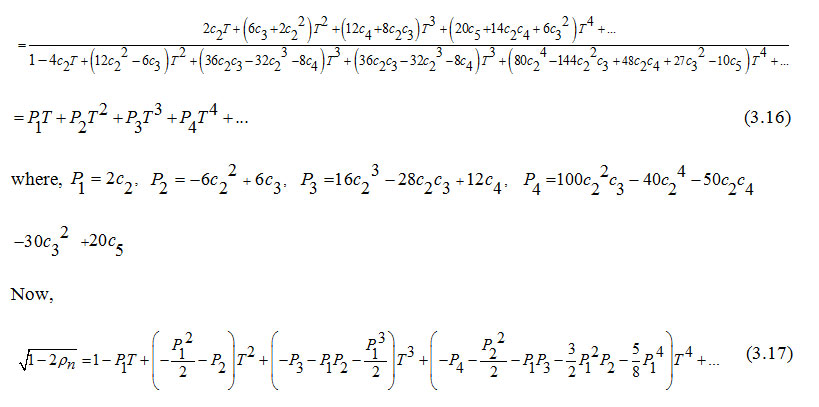
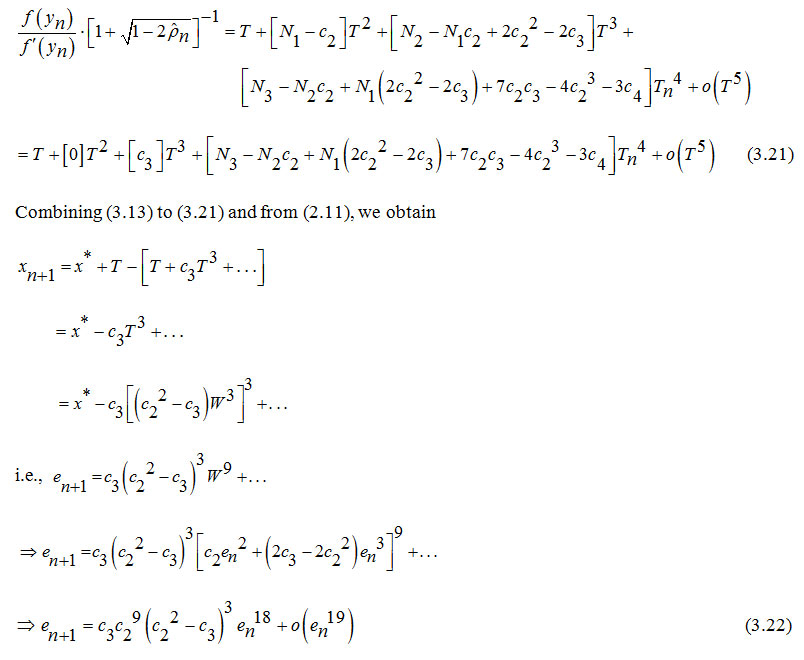
Hence, this method has eighteenth order convergence and its efficiency index is 8√18=1.4352.

Case 3.1: By expanding √1-2pn appearing in the denominator of the third step of algorithm 2.1, we obtain

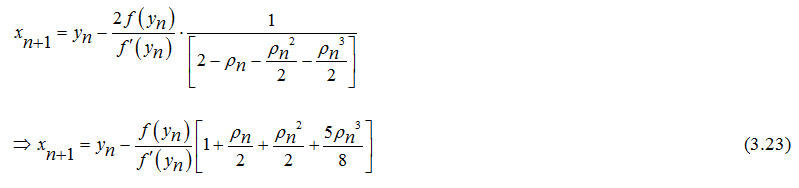
where pn is as given in (2.12).

Considering the first degree and second degree terms of  the expression lying within the square brackets of the formula (3.23) and from the algorithm 2.1, we have the following two more algorithms.

Algorithm 3.1: For a given x_0, compute x_n+1 by the iterative schemes

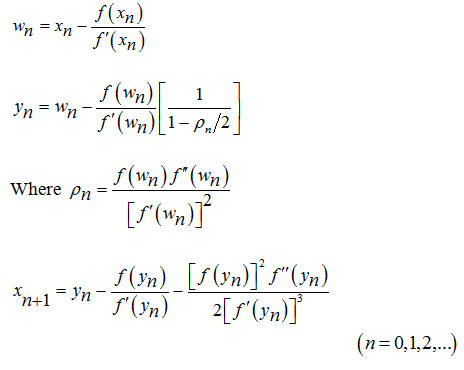
which is same as the eighteenth order convergent method proposed by Mohammed and Hafiz [10].

Algorithm 3.2: For a given x₀, compute x_n+1 by the iterative schemes

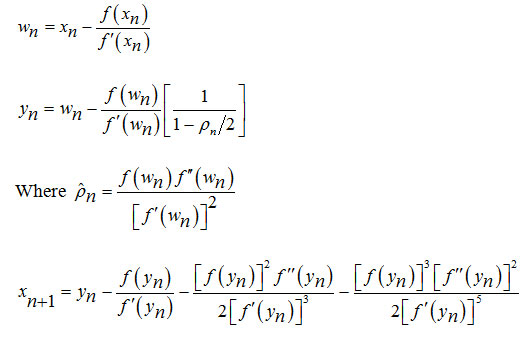
As done in convergence criteria above in section 3, one can easily obtain e_n+1 αe_n¹⁸. Therefore, the algorithm (3.2) has eighteenth order convergence.

Numerical Examples

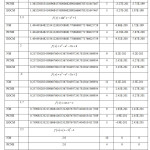
We consider the same examples considered by Mohammed and Hafiz [10] and compared EOCM with NM and PCNH methods. The computations are carried out by using mpmath-PYTHON software programming and comparison of number of iterations for these methods are obtained such that

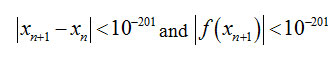
The above computational results exhibit the superiority of the new method EOCM over the Newton’s method and PCNH method in terms of number of iterations and accuracy.

Table 1: Comparison of different methods   Click here to View table

 

References

1. I.K. Argyros, S.K. Khattri, An improved semi local convergence analysis for the Chebyshev method, Journal of Applied Mathematics and computing, 42, No-s: 1, 2 (2013), 509-528, doi: 10.1007/s12190-013-0647-3.
   CrossRef
2. M.A. Hafiz, Solving nonlinear equations using steffensen-type methods with optimal order of convergence, Palestine Journal of Mathematics, 3, No: 1  (2014), 113-119.
3. M.A. Hafiz, A new combined bracketing method for solving nonlinear equations, Journal of  Mathematical and Computational Science,  3,  No.1 (2013)..
4. M.A. Hafiz, S.M.H. Al-Goria,  Solving nonlinear equations using a new tenth-and seventh- order methods free from second derivative, International Journal of Differential Equations and Applications,  12, No. 3 (2013), 169-183,2013, doi: 10.12732/ijdea.v12i3.1344.
5. S.K. Khattri, Torgrim Log, Constructing third-order derivative-free iterative methods, Int. J. Comput. Math., 88, No. 7 (2011), 1509-1518, doi: 10.1080/00207160.2010520705.
6. S.K. Khattri, Quadrature based optimal iterative methods with applications in high precision computing,  Numer. Math. Theor. Meth. Appl., 5 (2012), 592-601.
   CrossRef
7. S.K. Khattri, Trond Steihaug, Algorithm for forming derivative-free optimal methods, , Numerical Algorithms, (2013),  doi: 10.1007/s11075-013-9715-x.
   CrossRef
8. Mohamed S.M. Bahgat, M.A. Hafiz,  New two-step predictor-corrector method with ninth order convergence for solving nonlinear equations, Journal of Advances in Mathematics ,  2 (2013), 432-437.
9. Khalida Inayat Noor, Muhammad Aslam Noor, Shaher Momani, Modified Householder iterative methods for nonlinear equations”, Applied Mathematics and Computation, 190 (2007), 1534-1539, doi: 10.1016/j.amc.2007.02.036.
   CrossRef
10. Mohamed S.M. Bahgat, M.A. Hafiz,  Three-step iterative method with eighteenth order convergence for solving nonlinear equations, Int. Journal of Pure and Applied Mathematics, Vol. 93, No. 1, 2014, 85-94.
11. Vatti V.B.Kumar,  Mylapalli M. S. Kumar, Katragadda A. Kumari,Extrapolated Newton- Raphson Method, Math. Educ. 43, No. 1, 103-108 (2009).

---

This work is licensed under a Creative Commons Attribution 4.0 International License.